Residue class-wise affine group

In mathematics, residue class-wise affine groups are certain permutation groups acting on $\mathbb{Z}$ (the integers), whose elements are bijective residue class-wise affine mappings.

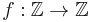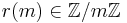A mapping $f: \mathbb{Z} \rightarrow \mathbb{Z}$ is called residue class-wise affine if there is a nonzero integer $m$ such that the restrictions of $f$ to the residue classes (mod $m$ ) are all affine. 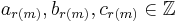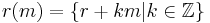This means that for any residue class $r(m) \in \mathbb{Z}/m\mathbb{Z}$ there are coefficients $a_{r(m)}, b_{r(m)}, c_{r(m)} \in \mathbb{Z}$ such that the restriction of the mapping $f$ to the set $r(m) = \{r %2B km | k \in \mathbb{Z}\}$ is given by

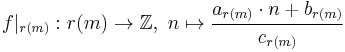$f|_{r(m)}: r(m) \rightarrow \mathbb{Z}, \ n \mapsto \frac{a_{r(m)} \cdot n %2B b_{r(m)}}{c_{r(m)}}$ .

Residue class-wise affine groups are countable, and they are accessible to computational investigations. Many of them act multiply transitively on $\mathbb{Z}$ or on subsets thereof. Only relatively basic facts about their structure are known so far.

See also the Collatz conjecture, which is an assertion about a surjective, but not injective residue class-wise affine mapping.

References and external links

Stefan Kohl. Restklassenweise affine Gruppen. Dissertation, Universität Stuttgart, 2005.Archivserver Deutsche Bibliothek

OPUS-Datenbank(Universität Stuttgart)

Stefan Kohl. RCWA - Residue Class-Wise Affine Groups. GAP package. 2005.